Priemgetallen
Ik las ergens dat er priemgetallen zijn zich herhalen na (n-1) cijfers achter de komma.
Hierbij staat "n" dus voor het priemgetal.
Bijvoorbeeld: als je 1 deelt door 17, herhaalt de breuk zich na 16 cijfers:
1/17 = 0,05882352941176470588235294117647 etc.
Als je nu een vierkant maakt van 16x16 hokjes en je zet in de eerste rij de cijfers achter de komma van
de breuk 1/17,in de tweede rij 2/17..... tot de zestiende rij = 16/17, dan krijg je dit:
Wat kunnen we hieraan zien?
Op iedere regel komen dezelfde getallen voor, de 16 reperterende cijfers achter de komma van 1/17.
Op iedere regel staan ze in de zelfde volgorde, maar steeds beginnen ze met een ander getal; logisch,
het is een steeds groter wordende breuk.
Net als met het Vedisch Vierkant begon ik te spelen met dit vierkant.
Maak alle nullen zwart; de enen, de twee�n, etc.
En toen ontdekte ik nog iets: als je de nullen en negens zwart maakt, dan ontstaat er een symmetrisch figuur.
Zo ook bij 1 en 8; 2 en 7; 3 en 6; 4 en 5.
Want ik ontdekte dat als er in die rij van 16 getallen op bijvoorbeeld de tweede positie een 3 staat,
dan staat er acht posities verder een 6. Idem voor de andere getallenparen.
De volgende plaatjes laten deze symmetrische figuren zien:

17-09 |

17-18 |

17-27 |

17-36 |

17-45 |
Nou, en daar ben ik verder mee gaan werken.
Andere priemgetallen (onder de 100) waarvoor geldt dat de breuk zich herhaalt na n-1 zijn:
7, 17, 19, 23, 29, 47, 59, 61, 97.
Maar er zijn ook priemgetallen waarvan de breuk zich herhaalt na (n-1)/2 getallen.
Hiervan is 13 een voorbeeld:
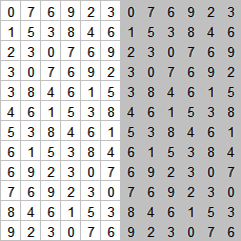
In dit geval zijn er dus 2 verschillende cijferreeksen die zich herhalen:
De rijen 1, 3, 4, 9, 10 en 12 zijn de verschillende volgordes van de getallenreeks 0 7 6 9 2 3
De rijen 2, 5, 6, 7, 8 en 11 zijn de verschillende volgordes van de getallenreeks 1 5 3 8 4 6
Andere priemgetallen (onder de 100) die zich herhalen na (n-1)/2 zijn:
31, 43, 67, 71, 83 en 89
Dan zijn er (opnieuw, onder de 100) ook nog een paar vreemde eenden in de bijt:
De breuk van het priemgetal 11 herhaalt zich na 2 getallen (n-1)/5
die van 37 na 3 (n-1)/12
die van 41 na 5 (n-1)/8
die van 53 na 13 (n-1)/4
die van 73 na 8 (n-1)/9
die van 79 na 13 (n-1)/6
Ik heb op basis van de getallencombinaties 09-18-27-36-45 binnen de priemgetallen allerlei patronen uitgewerkt, die ik op
deze website laat zien!
Voor de navigatie: hier nogmaals de links naar de verschillende pagina's:
Naar boven







